Finanzmodelle
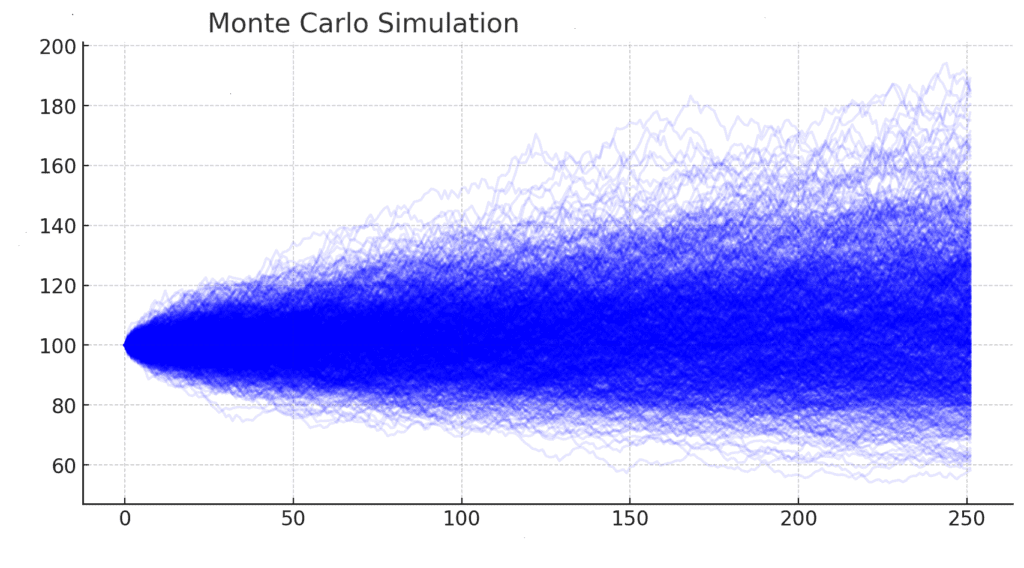
Monte-Carlo-Simulation in der Finanzmodellierung: So lassen sich Risiken und Renditen vorhersagen
In der Finanzwelt ist Unsicherheit die einzige Gewissheit. Ob Portfoliomanager, Finanzanalyst oder Unternehmer – die Vorhersage zukünftiger Ergebnisse ist ein entscheidender Bestandteil der Entscheidungsfindung. Traditionelle Finanzmodelle basieren oft auf deterministischen Ansätzen, die von festen Input- und Output-Größen ausgehen.
Die reale Welt ist jedoch weitaus komplexer, mit unzähligen Variablen, die die Ergebnisse beeinflussen. Hier Monte-Carlo-Simulation ins Spiel – ein leistungsstarkes Tool, mit dem Sie die Unsicherheit und Variabilität modellieren können, die Finanzsystemen innewohnt.
Was ist eine Monte-Carlo-Simulation?
Die Monte-Carlo-Simulation ist ein statistisches Verfahren, das Zufallsstichproben und statistische Modellierung nutzt, um mathematische Funktionen abzuschätzen und die Funktionsweise komplexer Systeme nachzubilden. Benannt nach dem berühmten Casino von Monte Carlo, dessen inhärenter Zufall und Zufallsprinzip dafür verantwortlich sind, hat sich diese Methode zu einem Eckpfeiler der Finanzmodellierung entwickelt.
Die Essenz der Monte-Carlo-Simulation
Im Kern generiert die Monte-Carlo-Simulation viele mögliche Szenarien für einen gegebenen Prozess, jedes basierend auf zufälligen Eingaben. Durch die Analyse der Ergebnisse dieser Szenarien erhält man ein probabilistisches Verständnis des Systemverhaltens. Dies ist besonders im Finanzwesen nützlich, wo Variablen wie Marktrenditen, Zinssätze und Konjunkturindikatoren unsicher sind.
Historischer Kontext
Die Monte-Carlo-Methode wurde 1964 erstmals von David B. Hertz in seinem Artikel in der Harvard Business Review in die Finanzwelt eingeführt, in dem er ihre Anwendung im Unternehmensfinanzwesen erörterte. 1977 leistete Phelim Boyle in seinem bahnbrechenden Artikel im Journal of Financial Economics Pionierarbeit bei der Simulation der Derivatebewertung.
Warum Monte-Carlo-Simulationen in der Finanzmodellierung verwenden?
Monte-Carlo-Simulationen finden in der Finanzwelt ein breites Anwendungsspektrum und helfen bei der Bewertung verschiedener Finanzinstrumente und Anlagestrategien.
1. Portfoliobewertung
Anleger nutzen Monte-Carlo-Simulationen, um die potenzielle zukünftige Performance ihrer Anlageportfolios zu bewerten. Simulationen können mögliche Portfoliowerte im Zeitverlauf prognostizieren, indem sie das zufällige Verhalten von Vermögenspreisen und deren Korrelationen modellieren. Dies hilft, die Wahrscheinlichkeit des Erreichens bestimmter finanzieller Ziele zu verstehen und fundierte Anlageentscheidungen zu treffen.
2. Risikobewertung
Risikomanagement ist im Finanzwesen von größter Bedeutung. Monte-Carlo-Simulationen ermöglichen es Analysten, die Auswirkungen von Risiken und Unsicherheiten in Finanzmodellen zu quantifizieren. Durch die Simulation verschiedener Risikofaktoren – wie Marktbedingungen, Zinssätze und Konjunkturindikatoren – können Analysten die Wahrscheinlichkeit verschiedener negativer Ergebnisse abschätzen und Strategien zur Minderung potenzieller Verluste entwickeln.
3. Optionspreisgestaltung
Die Bewertung komplexer Finanzderivate, insbesondere von Optionen, kann aufgrund ihrer pfadabhängigen Natur eine Herausforderung darstellen. Monte-Carlo-Methoden werden häufig zur Preisbestimmung dieser Derivate eingesetzt. Dabei werden verschiedene mögliche Kursverläufe des Basiswerts simuliert und die entsprechenden Auszahlungen berechnet. Dieser Ansatz eignet sich besonders für die Preisgestaltung exotischer Optionen ohne geschlossene Lösungen.
4. Kapitalbudgetierung und Projektfinanzierung
In der Unternehmensfinanzierung werden Monte-Carlo-Simulationen eingesetzt, um die Rentabilität großer Projekte zu bewerten. Durch die Modellierung von Unsicherheiten bei Cashflows, Diskontsätzen und anderen Variablen können Unternehmen die Wahrscheinlichkeitsverteilung des Nettobarwerts (NPV) oder des internen Zinsfußes (IRR) eines Projekts abschätzen. Diese probabilistischen Erkenntnisse helfen dabei, fundierte Entscheidungen zur Investitionsplanung zu treffen.
So funktioniert die Monte-Carlo-Simulation: Eine Schritt-für-Schritt-Anleitung
Lassen Sie uns den Prozess der Durchführung einer Monte-Carlo-Simulation in der Finanzmodellierung aufschlüsseln:
- Schritt 1: Definieren Sie das Problem und identifizieren Sie Variablen: Definieren Sie zunächst klar das Problem, das Sie lösen möchten. Identifizieren Sie die wichtigsten Eingabevariablen, die das Ergebnis beeinflussen. Wenn Sie beispielsweise Aktienrenditen modellieren, könnten die Variablen die erwartete Rendite, die Volatilität und den Zeithorizont umfassen.
- Schritt 2: Wahrscheinlichkeitsverteilungen angeben: Weisen Sie jeder Eingabevariable Wahrscheinlichkeitsverteilungen zu. Gängige Verteilungen sind:
- Normalverteilung: Für Variablen wie Aktienrenditen.
- Lognormalverteilung: Für Variablen, die nicht negativ sein können, wie z. B. Aktienkurse.
- Gleichmäßige Verteilung: Wenn alle Ergebnisse gleich wahrscheinlich sind.
- Schritt 3: Zufallsstichproben generieren: Verwenden Sie einen Zufallszahlengenerator, um Tausende oder Millionen von Zufallsstichproben für jede Eingabevariable basierend auf ihren angegebenen Verteilungen zu erstellen.
- Schritt 4: Simulationen ausführen: Berechnen Sie das Ergebnis mithilfe Ihres Finanzmodells für jeden Satz von Zufallsstichproben. Wenn Sie beispielsweise Portfoliorenditen modellieren, können Sie die folgende Formel verwenden:

- Schritt 5: Ergebnisse analysieren: Fassen Sie die Ergebnisse aller Simulationen zusammen, um eine Wahrscheinlichkeitsverteilung der Ergebnisse zu erstellen. Analysieren Sie wichtige Kennzahlen wie Mittelwert, Median, Standardabweichung und Perzentile.
- Schritt 6: Interpretieren und Entscheidungen treffen: Nutzen Sie die Ergebnisse, um Risiken zu bewerten, mögliche Ergebnisse zu identifizieren und fundierte Entscheidungen zu treffen. Sie können beispielsweise die Wahrscheinlichkeit für das Erreichen einer Zielrendite oder die Wahrscheinlichkeit eines Worst-Case-Szenarios ermitteln.
Beispiel: Monte-Carlo-Simulation für Portfoliorenditen
Betrachten wir ein einfaches Beispiel eines Portfolios, das aus zwei Vermögenswerten besteht: Aktie A und Aktie B. Wir möchten die zukünftigen Renditen dieses Portfolios über einen bestimmten Zeithorizont, sagen wir 10 Jahre, mithilfe einer Monte-Carlo-Simulation simulieren.
Schritt 1: Definieren Sie das Portfolio
- Aktie A: Erwartete jährliche Rendite = 8%, Standardabweichung = 15%
- Aktie B: Erwartete jährliche Rendite = 12%, Standardabweichung = 20%
- Korrelation zwischen Aktie A und Aktie B: 0.5
- Portfoliogewichtungen: 60% im Lager A und 40% im Lager B
Schritt 2: Zufällige Renditen generieren
Wir werden zufällige Renditen für die Aktien A und B basierend auf ihren erwarteten Renditen generieren, Standardabweichungenund Korrelation. Wir können eine multivariate Normalverteilung verwenden, um korrelierte Zufallsrenditen zu generieren.
Schritt 3: Portfoliowachstum simulieren
Wir können das Wachstum des Portfolios über die 10 Jahre simulieren, indem wir die jährlichen Renditen zusammenrechnen.
Schritt 4: Ergebnisse analysieren
Nachdem wir die Simulation ausgeführt haben, können wir die Ergebnisse analysieren, um die Verteilung der möglichen Portfoliowerte nach 10 Jahren zu verstehen.
Schritt 5: Interpretieren Sie die Ergebnisse
- Durchschnittlicher endgültiger Portfoliowert: Der durchschnittliche Portfoliowert nach 10 Jahren über alle Simulationen hinweg.
- Medianer endgültiger Portfoliowert: Der mittlere Wert des Portfolios nach 10 Jahren, der weniger von extremen Ergebnissen beeinflusst werden kann.
- Standardabweichung: Ein Maß für die Streuung der endgültigen Portfoliowerte, das das mit dem Portfolio verbundene Risiko angibt.
Herausforderungen in der Monte-Carlo-Simulation meistern
Obwohl die Monte-Carlo-Simulation ein leistungsstarkes Tool zur Finanzmodellierung ist, bringt sie auch spezielle Herausforderungen mit sich, die Fachleute bewältigen müssen, um genaue und aussagekräftige Ergebnisse zu gewährleisten.
1. Auswahl der richtigen Wahrscheinlichkeitsverteilungen
Die Auswahl geeigneter Wahrscheinlichkeitsverteilungen für die Eingabevariablen ist entscheidend. Ein häufiger Fehler ist die Annahme einer Normalverteilung für alle Finanzvariablen, die nicht immer zutreffend ist. Beispiel:
- Aktienrenditen: Wird häufig mit einer logarithmischen Normalverteilung statt einer Normalverteilung modelliert, da Aktienkurse nicht negativ sein können.
- Zinssätze: Kann einem Mittelwert-Rückkehrprozess wie dem Ornstein-Uhlenbeck-Modell folgen.
- Rohstoffpreise Sie weisen häufig Schiefe und Wölbung auf, was Annahmen zur Standardverteilung problematisch macht.
Tipp: Verwenden Sie historische Daten und statistische Analysen, um die am besten passende Verteilung für jede Variable zu bestimmen.
2. Umgang mit Korrelationen zwischen Variablen
Finanzielle Variablen sind oft voneinander abhängig. Das Ignorieren von Korrelationen kann zu irreführenden Ergebnissen führen. Beispielsweise weisen Aktienrenditen und Zinssätze in der Regel inverse Beziehungen auf.
Lösung:
- Verwenden Sie ein Korrelationsmatrix um Abhängigkeiten zwischen Variablen zu modellieren.
- Beschäftigen Cholesky-Zerlegung um korrelierte Zufallsvariablen in der Simulation zu erzeugen.
3. Rechenkomplexität und Leistung
Monte-Carlo-Simulationen erfordern die Ausführung von Tausenden oder sogar Millionen von Iterationen, was rechenintensiv sein kann.
Optimierungen:
- Verwenden Techniken zur Varianzreduzierung wie zum Beispiel antithetische Variablen oder Wichtigkeitsstichproben um die Effizienz zu verbessern.
- Parallelisieren Sie Berechnungen mit Pythons Mehrfachverarbeitung oder Excel VBA-Makros.
4. Ergebnisse richtig interpretieren
Eine der größten Gefahren besteht darin, die Ergebnisse falsch zu interpretieren. Nur weil die Wahrscheinlichkeit eines bestimmten Szenarios gering ist, heißt das nicht, dass es nicht eintreten wird.
Bewährte Methoden:
- Schauen Sie sich die Extremrisiko (z. B. 5%-Worst-Case-Szenario), anstatt sich ausschließlich auf den Mittelwert oder Median zu konzentrieren.
- Erwägen Sie das Laufen Stresstests um zu sehen, wie sich das Modell unter extremen Bedingungen verhält.
So führen Sie eine Monte-Carlo-Simulation in Excel und Python durch
Mit speziellen Funktionen und Werkzeugen können Monte-Carlo-Simulationen implementiert werden in Excel Und Python.
1. Monte-Carlo-Simulation in Excel
Excel ist ein hervorragendes Tool für schnelle und zugängliche Monte-Carlo-Simulationen.
Schritte:
- Definieren Sie das Modell
- Entscheiden Sie sich für eine Formel oder einen Prozess mit unsicheren Variablen (z. B. Vorhersage von Aktienkursen oder Projektkosten).
- Eingabe von Zufallsvariablen
- Verwenden Sie =RAND() für gleichmäßige Zufallszahlen zwischen 0 und 1.
- Verwenden Sie =NORM.INV(RAND(), Mittelwert, Standardabweichung) für normalverteilte Werte.
- Simulieren Sie mehrere Szenarien
- Ziehen Sie die Formel nach unten, um Tausende zufälliger Szenarien zu generieren.
- Berechnen Sie wichtige Statistiken
- Berechnen Sie den Mittelwert, die Standardabweichung und andere relevante Messwerte mithilfe von Excel-Funktionen.
- Analysieren Sie Ergebnisse mit Histogrammen
- Verwenden Sie Excel Datenanalyse-ToolPak um ein Histogramm zu erstellen.
Beispiel: Aktienkurssimulation
Nehmen wir an, die erwartete Rendite einer Aktie beträgt 7% mit einem 15% Standardabweichung über ein Jahr.
- In der Zelle A1, geben Sie den Startpreis ein: 100
- In B1, geben Sie die Formel für den Preis des nächsten Jahres ein
- Ziehen Sie diese Formel nach unten auf 1000 Szenarien simulieren.
- Berechnen:
- Durchschnittspreis: =DURCHSCHNITT(B1:B1000)
- Standardabweichung: =STABW(B1:B1000)
2. Monte-Carlo-Simulation in Python
Python bietet eine robustere und flexiblere Möglichkeit, Monte-Carlo-Simulationen mit NumPy, Pandas und Matplotlib auszuführen.
Beispiel: Aktienkurssimulation
Wann sollte man Excel und wann Python verwenden?
| Besonderheit | Excel | Python |
| Benutzerfreundlichkeit | Einfach für kleine Modelle | Besser für groß angelegte Simulationen |
| Leistung | Langsamer bei großen Datensätzen | Schneller und effizienter |
| Flexibilität | Eingeschränkte Statistikfunktionen | Mehr Anpassungsmöglichkeiten (NumPy, SciPy) |
| Visualisierung | Grundlegende Diagramme | Erweitertes Plotten (Matplotlib, Seaborn) |
Praktische Tipps für eine effektive Monte-Carlo-Simulation
- Einfach anfangen: Beginnen Sie mit einem Basismodell und steigern Sie die Komplexität schrittweise, wenn Sie sicherer werden.
- Eingaben validieren: Stellen Sie sicher, dass Ihre Eingabevariablen und Verteilungen realistisch sind und auf zuverlässigen Daten basieren.
- Führen Sie genügend Simulationen durch: Die Genauigkeit Ihrer Ergebnisse hängt von der Anzahl der Simulationen ab. Streben Sie mindestens 10.000 Iterationen an.
- Sensitivitätsanalyse verwenden: Identifizieren Sie, welche Variablen die Ergebnisse am stärksten beeinflussen.
- Dokumentannahmen: Dokumentieren Sie alle Annahmen und Einschränkungen Ihres Modells.
Fallstudie: Monte-Carlo-Simulation bei der Projektbewertung mithilfe eines Finanzmodells
In dieser Fallstudie werden wir ein hypothetisches Infrastrukturprojekt mithilfe der Monte-Carlo-Simulation bewerten, um die Nettogegenwartswert (NPV), angesichts der Unsicherheit bei wichtigen Finanzparametern wie Anfangsinvestition, Umsatzwachstum, Betriebskosten und Diskontsatz.
Projektübersicht
- Projektname: Grünes Energiekraftwerk
- Projektdauer: 10 Jahre
- Erstinvestition: $50 Millionen
- Jährliche Umsatzwachstumsrate: 5% (±2%)
- Betriebskosten: 301 TP3T Umsatz (±51 TP3T)
- Diskontsatz: 8% (±1%)
Mithilfe der Monte-Carlo-Simulation können Sie die Bandbreite möglicher Kapitalwerte analysieren und Erkenntnisse zur finanziellen Tragfähigkeit des Projekts unter verschiedenen Szenarien gewinnen.
Aufbau der Monte-Carlo-Simulation
So führen Sie die Simulation durch:
- Wahrscheinlichkeitsverteilungen definieren für wichtige finanzielle Inputs:
- Umsatzwachstumsrate: Normalverteilung (Mittelwert = 5%, Standardabweichung = 2%)
- Betriebskosten als % des Umsatzes: Normalverteilung (Mittelwert = 30%, Standardabweichung = 5%)
- Diskontsatz: Normalverteilung (Mittelwert = 8%, Standardabweichung = 1%)
- Führen Sie 10.000 Simulationen durch, wobei der NPV für jeden Lauf berechnet wird.
- Ergebnisse zusammenfassen mithilfe statistischer Messungen und Visualisierungen.
Jetzt werde ich die Monte-Carlo-Simulation ausführen und die Ergebnisse generieren.
Monte-Carlo-Simulation: NPV-Verteilung
Ergebnisse der Monte-Carlo-Simulation
| Wachstumsrate | Betriebskosten % | Diskontsatz | |
| zählen | 10000.0 | 10000.0 | 10000.0 |
| bedeuten | 0.050040570362915315 | 0.3002260181128686 | 0.07997808603004744 |
| Standard | 0.019910554247468792 | 0.04968107384600725 | 0.01008925573859806 |
| Min | -0.01856183610533345 | 0.11544796696907525 | 0.04046458542990874 |
| 25% | 0.03640861533085948 | 0.26678017932445197 | 0.07319111966613821 |
Die Ergebnisse der Monte-Carlo-Simulation sind nun verfügbar. Das Histogramm zeigt die Verteilung der Nettobarwertergebnisse (NPV) und verdeutlicht die finanzielle Unsicherheit des Projekts. Sie können auch die zusammenfassende Statistiktabelle einsehen, um wichtige Erkenntnisse wie Mittelwert, Standardabweichung und Perzentilwerte für NPV, Wachstumsrate, Betriebskosten und Diskontsatz zu überprüfen. Kontaktieren Sie mich, wenn Sie weitere Analysen oder Interpretationen benötigen!
Fazit: Warum die Monte-Carlo-Simulation ein Wendepunkt ist
Monte-Carlo-Simulation ist eines der effektivsten Tools zur Risikobewertung und FinanzprognoseIm Gegensatz zu herkömmlichen statischen Modellen bietet es eine probabilistische Sicht auf mögliche Ergebnisseund hilft Investoren und Unternehmen, datenbasierte Entscheidungen zu treffen.
Um Monte-Carlo-Simulationen zu vereinfachen und die Genauigkeit zu verbessern, SHEETS.MARKET bietet professionelle Vorlagen die Ihnen Folgendes ermöglichen:
- Führen Sie Tausende von Simulationen durch mit nur wenigen Klicks.
- Visualisieren Sie Risikoverteilungen sofort.
- Anpassen von Modellen für Ihre finanziellen Bedürfnisse.
🚀 Sparen Sie Zeit und steigern Sie die Präzision – erkunden Sie Tabellen.Markt Fordern Sie noch heute professionelle Tools zur Finanzmodellierung an! Für weitere Einblicke in Finanzmodellierung, Risikoanalyse und Monte-Carlo-Simulationen folgen Sie uns auf LinkedIn. Beteiligen Sie sich an der Diskussion und erfahren Sie, wie diese Tools Ihren Entscheidungsprozess unterstützen können.