Финансовые модели
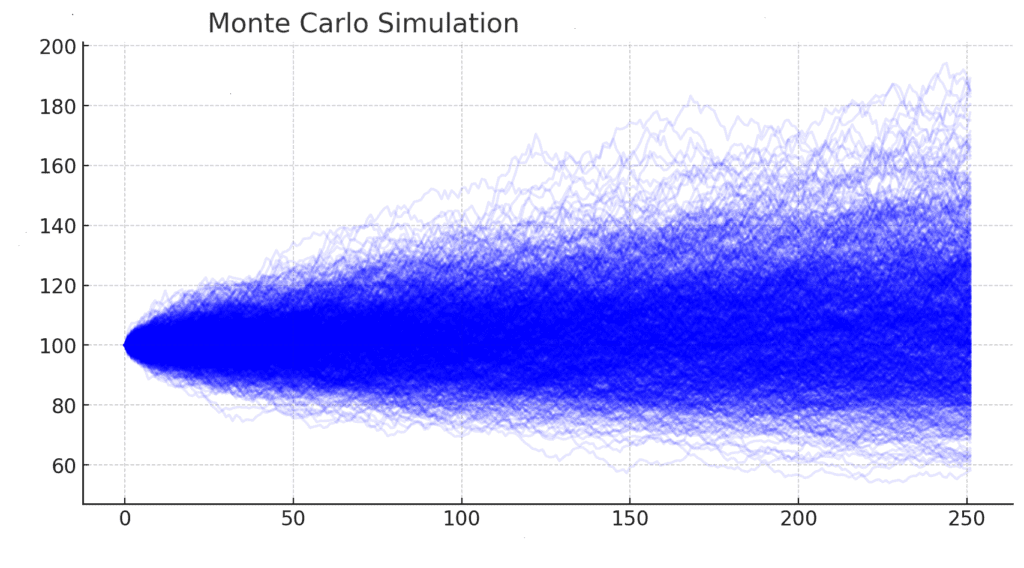
Моделирование Монте-Карло в финансовом моделировании: как прогнозировать риск и доходность
В мире финансов неопределенность — единственная определенность. Независимо от того, являетесь ли вы управляющим портфелем, финансовым аналитиком или владельцем бизнеса, прогнозирование будущих результатов является важнейшей частью принятия решений. Традиционные финансовые модели часто опираются на детерминированные подходы, которые предполагают фиксированные входы и выходы.
Однако реальный мир гораздо сложнее, в нем бесчисленное множество переменных, влияющих на результаты. Вот где Моделирование Монте-Карло в игру вступает мощный инструмент, позволяющий моделировать неопределенность и изменчивость, присущие финансовым системам.
Что такое моделирование методом Монте-Карло?
Моделирование Монте-Карло — это статистический метод, который использует случайную выборку и статистическое моделирование для оценки математических функций и имитации операций сложных систем. Названный в честь знаменитого казино Монте-Карло из-за присущей ему случайности и случайности, этот метод стал краеугольным камнем в финансовом моделировании.
Суть моделирования Монте-Карло
По своей сути, моделирование Монте-Карло генерирует множество возможных сценариев для заданного процесса, каждый из которых основан на случайных входных данных. Анализируя результаты этих сценариев, можно получить вероятностное понимание поведения системы. Это особенно полезно в финансах, где такие переменные, как рыночная доходность, процентные ставки и экономические показатели, являются неопределенными.
Исторический контекст
Метод Монте-Карло был впервые представлен в финансах в 1964 году Дэвидом Б. Герцем в его статье в Harvard Business Review, в которой он обсуждал его применение в корпоративных финансах. В 1977 году Фелим Бойл стал пионером моделирования в оценке производных инструментов в своей основополагающей статье в Journal of Financial Economics.
Зачем использовать метод Монте-Карло в финансовом моделировании?
Моделирование по методу Монте-Карло имеет широкий спектр применения в финансах, помогая оценивать различные финансовые инструменты и инвестиционные стратегии.
1. Оценка портфеля
Инвесторы используют моделирование Монте-Карло для оценки потенциальной будущей эффективности своих инвестиционных портфелей. Моделирование может прогнозировать возможные значения портфеля с течением времени, моделируя случайное поведение цен на активы и их корреляции. Это помогает понять вероятность достижения определенных финансовых целей и принимать обоснованные инвестиционные решения.
2. Оценка риска
Управление рисками имеет первостепенное значение в финансах. Моделирование Монте-Карло позволяет аналитикам количественно оценить влияние риска и неопределенности в финансовых моделях. Аналитики могут оценить вероятность различных неблагоприятных исходов, моделируя различные факторы риска, такие как рыночные условия, процентные ставки и экономические показатели, и разработать стратегии для снижения потенциальных потерь.
3. Ценообразование опционов
Оценка сложных финансовых деривативов, в частности опционов, может быть сложной из-за их зависимой от пути природы. Методы Монте-Карло широко используются для оценки этих деривативов путем моделирования многочисленных путей, по которым может пойти цена базового актива, и расчета соответствующих выплат. Этот подход особенно полезен для оценки экзотических опционов, не имеющих решений в закрытой форме.
4. Составление бюджета капиталовложений и проектное финансирование
В корпоративных финансах моделирование Монте-Карло используется для оценки жизнеспособности крупных проектов. Моделируя неопределенности в денежных потоках, ставках дисконтирования и других переменных, компании могут оценить распределение вероятностей чистой приведенной стоимости (NPV) или внутренней нормы доходности (IRR) проекта. Это вероятностное понимание помогает принимать обоснованные решения по бюджетированию капиталовложений.
Как работает моделирование Монте-Карло: пошаговое руководство
Давайте разберем процесс проведения моделирования Монте-Карло в финансовом моделировании:
- Шаг 1: Определите проблему и определите переменные: Начните с четкого определения проблемы, которую вы хотите решить. Определите ключевые входные переменные, которые влияют на результат. Например, если вы моделируете доходность акций, переменные могут включать ожидаемую доходность, волатильность и временной горизонт.
- Шаг 2: Укажите распределения вероятностей: Назначьте распределения вероятностей для каждой входной переменной. Распространенные распределения включают:
- Нормальное распределение: Для таких переменных, как доходность акций.
- Логнормальное распределение: Для переменных, которые не могут быть отрицательными, например, цены акций.
- Равномерное распределение: Когда все результаты равновероятны.
- Шаг 3: Генерация случайных выборок: Используйте генератор случайных чисел для создания тысяч или миллионов случайных выборок для каждой входной переменной на основе их заданных распределений.
- Шаг 4: Запуск моделирования: Рассчитайте результат, используя вашу финансовую модель для каждого набора случайных выборок. Например, если вы моделируете доходность портфеля, вы можете использовать формулу:

- Шаг 5: Анализ результатов: Объедините результаты всех симуляций, чтобы создать распределение вероятностей результатов. Проанализируйте ключевые показатели, такие как среднее значение, медиана, стандартное отклонение и процентили.
- Шаг 6: Интерпретация и принятие решений: Используйте результаты для оценки риска, выявления потенциальных результатов и принятия обоснованных решений. Например, вы можете определить вероятность достижения целевого дохода или вероятность наихудшего сценария.
Пример: моделирование доходности портфеля по методу Монте-Карло
Рассмотрим простой пример портфеля, состоящего из двух активов: акций A и акций B. Мы хотим смоделировать будущую доходность этого портфеля за определенный период времени, скажем, 10 лет, используя моделирование по методу Монте-Карло.
Шаг 1: Определите портфель
- Акция А: Ожидаемая годовая доходность = 8%, стандартное отклонение = 15%
- Акции B: Ожидаемая годовая доходность = 12%, стандартное отклонение = 20%
- Корреляция между акциями A и B: 0.5
- Вес портфеля: 60% в наличии A и 40% в наличии B
Шаг 2: Генерация случайных результатов
Мы сгенерируем случайную доходность для акций A и B на основе их ожидаемой доходности, стандартные отклоненияи корреляция. Мы можем использовать многомерное нормальное распределение для генерации коррелированных случайных возвратов.
Шаг 3: Моделирование роста портфеля
Мы можем смоделировать рост портфеля за 10 лет, суммируя годовую доходность.
Шаг 4: Анализ результатов
После запуска моделирования мы можем проанализировать результаты, чтобы понять распределение возможных значений портфеля через 10 лет.
Шаг 5: Интерпретация результатов
- Средняя окончательная стоимость портфеля: Средняя стоимость портфеля через 10 лет по всем расчетам.
- Медианная окончательная стоимость портфеля: Средняя стоимость портфеля через 10 лет, на которую экстремальные результаты могут повлиять в меньшей степени.
- Стандартное отклонение: Мера дисперсии итоговых значений портфеля, указывающая риск, связанный с портфелем.
Преодоление трудностей в моделировании Монте-Карло
Хотя моделирование по методу Монте-Карло является мощным инструментом финансового моделирования, оно сопряжено с определенными трудностями, которые специалисты должны решать для обеспечения точных и значимых результатов.
1. Выбор правильных распределений вероятностей
Выбор соответствующих распределений вероятностей для входных переменных имеет решающее значение. Распространенной ошибкой является предположение о нормальном распределении для всех финансовых переменных, что не всегда может быть точным. Например:
- Доходность акций: Часто моделируется с использованием логарифмически нормального распределения, а не нормального, поскольку цены акций не могут быть отрицательными.
- Процентные ставки: Может следовать процессу возврата к среднему значению, такому как модель Орнштейна-Уленбека.
- Цены на товары Часто проявляют асимметрию и эксцесс, что делает стандартные предположения о распределении проблематичными.
Кончик: Используйте исторические данные и статистический анализ, чтобы определить наиболее подходящее распределение для каждой переменной.
2. Обработка корреляций между переменными
Финансовые переменные часто взаимозависимы. Игнорирование корреляций может привести к вводящим в заблуждение результатам. Например, доходность акций и процентные ставки обычно демонстрируют обратные зависимости.
Решение:
- Используйте корреляционная матрица для моделирования зависимостей между переменными.
- Нанимать Разложение Холецкого для генерации коррелированных случайных величин в моделировании.
3. Сложность вычислений и производительность
Моделирование методом Монте-Карло требует выполнения тысяч или даже миллионов итераций, что может быть связано с большими вычислительными затратами.
Оптимизации:
- Использовать методы снижения дисперсии такой как антитетические вариаты или важность выборки для повышения эффективности.
- Распараллелить вычисления с помощью Python многопроцессорность или Excel's Макросы VBA.
4. Правильная интерпретация результатов
Одна из самых больших ловушек — неправильное толкование выходных данных. То, что определенный сценарий имеет низкую вероятность, не означает, что он не произойдет.
Лучшие практики:
- Посмотрите на хвостовой риск (например, 5% наихудший сценарий) вместо того, чтобы сосредоточиться исключительно на среднем значении или медиане.
- Рассмотрите возможность бега стресс-тесты чтобы увидеть, как модель ведет себя в экстремальных условиях.
Как выполнить моделирование Монте-Карло в Excel и Python
Используя специализированные функции и инструменты, моделирование Монте-Карло может быть реализовано в Эксель и Питон.
1. Моделирование Монте-Карло в Excel
Excel — превосходный инструмент для быстрого и доступного моделирования методом Монте-Карло.
Шаги:
- Определить модель
- Определитесь с формулой или процессом с неопределенными переменными (например, прогнозирование цен на акции или стоимости проекта).
- Входные случайные величины
- Используйте =RAND() для получения равномерных случайных чисел от 0 до 1.
- Используйте =NORM.INV(RAND(), mean, std_dev) для нормально распределенных значений.
- Моделируйте несколько сценариев
- Перетащите формулу вниз, чтобы сгенерировать тысячи случайных сценариев.
- Рассчитайте ключевые статистические данные
- Вычислите среднее значение, стандартное отклонение и другие соответствующие показатели с помощью функций Excel.
- Анализируйте результаты с помощью гистограмм
- Используйте Excel Пакет инструментов для анализа данных для создания гистограммы.
Пример: Моделирование цены акций
Предположим, что ожидаемая доходность акций составляет 7% с 15% стандартное отклонение более одного года.
- В клетке А1, введите начальную цену: 100
- В В1, введите формулу для цены следующего года
- Перетащите эту формулу вниз, чтобы смоделировать 1000 сценариев.
- Вычислить:
- Средняя цена: =СРЕДНЕЕ(B1:B1000)
- Стандартное отклонение: =СТАНДОТКЛОН(B1:B1000)
2. Моделирование Монте-Карло на Python
Python обеспечивает более надежный и гибкий способ выполнения моделирования Монте-Карло с использованием NumPy, Pandas и Matplotlib.
Пример: Моделирование цены акций
Когда использовать Excel, а когда Python
| Особенность | Эксель | Питон |
| Простота использования | Просто для моделей небольшого масштаба | Лучше подходит для крупномасштабного моделирования |
| Производительность | Медленнее с большими наборами данных | Быстрее и эффективнее |
| Гибкость | Ограниченные статистические функции | Больше настроек (NumPy, SciPy) |
| Визуализация | Базовые диаграммы | Расширенные возможности построения графиков (Matplotlib, Seaborn) |
Практические советы по эффективному моделированию методом Монте-Карло
- Начните с простого: Начните с базовой модели и постепенно усложняйте ее по мере обретения уверенности.
- Проверить входные данные: Убедитесь, что ваши входные переменные и распределения реалистичны и основаны на надежных данных.
- Проведите достаточно симуляций: Точность ваших результатов зависит от количества симуляций. Стремитесь к минимуму в 10 000 итераций.
- Используйте анализ чувствительности: Определите, какие переменные оказывают наиболее существенное влияние на результаты.
- Предположения документа: Задокументируйте все допущения и ограничения вашей модели.
Пример: Моделирование Монте-Карло при оценке проекта с использованием финансовой модели
В этом исследовании мы оценим гипотетический инфраструктурный проект, используя моделирование Монте-Карло для оценки Чистая приведенная стоимость (NPV), учитывая неопределенность ключевых финансовых параметров, таких как первоначальные инвестиции, рост доходов, эксплуатационные расходы и ставка дисконтирования.
Обзор проекта
- Название проекта: Экологически чистая энергетическая установка
- Продолжительность проекта: 10 лет
- Первоначальные инвестиции: $50 миллионов
- Темпы роста годового дохода: 5% (±2%)
- Эксплуатационные расходы: 30% дохода (±5%)
- Ставка дисконтирования: 8% (±1%)
Моделирование по методу Монте-Карло поможет проанализировать диапазон возможных значений чистой приведенной стоимости, предоставляя представление о финансовой жизнеспособности проекта при различных сценариях.
Настройка моделирования Монте-Карло
Для проведения моделирования:
- Определить распределение вероятностей для ключевых финансовых вложений:
- Темпы роста выручки: Нормальное распределение (среднее = 5%, стандартное отклонение = 2%)
- Эксплуатационные расходы как % выручки: Нормальное распределение (среднее = 30%, стандартное отклонение = 5%)
- Ставка дисконтирования: Нормальное распределение (среднее = 8%, стандартное отклонение = 1%)
- Запустите 10 000 симуляций, вычисляя NPV для каждого прогона.
- Подвести итоги с использованием статистических измерений и визуализаций.
Теперь я запущу моделирование по методу Монте-Карло и получу результаты.
Моделирование Монте-Карло: распределение NPV
Результаты моделирования Монте-Карло
| Темпы роста | Эксплуатационные расходы % | Ставка дисконтирования | |
| считать | 10000.0 | 10000.0 | 10000.0 |
| иметь в виду | 0.050040570362915315 | 0.3002260181128686 | 0.07997808603004744 |
| стандарт | 0.019910554247468792 | 0.04968107384600725 | 0.01008925573859806 |
| мин | -0.01856183610533345 | 0.11544796696907525 | 0.04046458542990874 |
| 25% | 0.03640861533085948 | 0.26678017932445197 | 0.07319111966613821 |
Результаты моделирования Монте-Карло теперь доступны. Гистограмма отображает распределение результатов чистой приведенной стоимости (NPV), подчеркивая финансовую неопределенность проекта. Вы также можете изучить сводную статистическую таблицу, чтобы просмотреть ключевые идеи, такие как среднее значение, стандартное отклонение и процентильные значения для NPV, темпы роста, эксплуатационные расходы и ставка дисконтирования. Дайте мне знать, если вам нужен дополнительный анализ или интерпретации!
Заключение: почему моделирование Монте-Карло меняет правила игры
Моделирование Монте-Карло один из самых эффективных инструментов оценки рисков и финансового прогнозирования. В отличие от традиционных статических моделей, он обеспечивает вероятностный взгляд на потенциальные результаты, помогая инвесторам и предприятиям принимать решения на основе данных.
Чтобы упростить моделирование Монте-Карло и повысить точность, SHEETS.MARKET предлагает профессиональные шаблоны которые позволяют вам:
- Проведите тысячи симуляций всего за несколько кликов.
- Визуализируйте распределение рисков немедленно.
- Настроить модели для ваших финансовых нужд.
🚀 Экономьте время и повышайте точность — исследуйте Листы.Маркет для профессиональных инструментов финансового моделирования уже сегодня! Для получения более подробной информации о финансовом моделировании, анализе рисков и моделировании Монте-Карло подпишитесь на нас LinkedInПрисоединяйтесь к обсуждению и узнайте, как эти инструменты могут помочь вам в процессе принятия решений.