Modelli finanziari
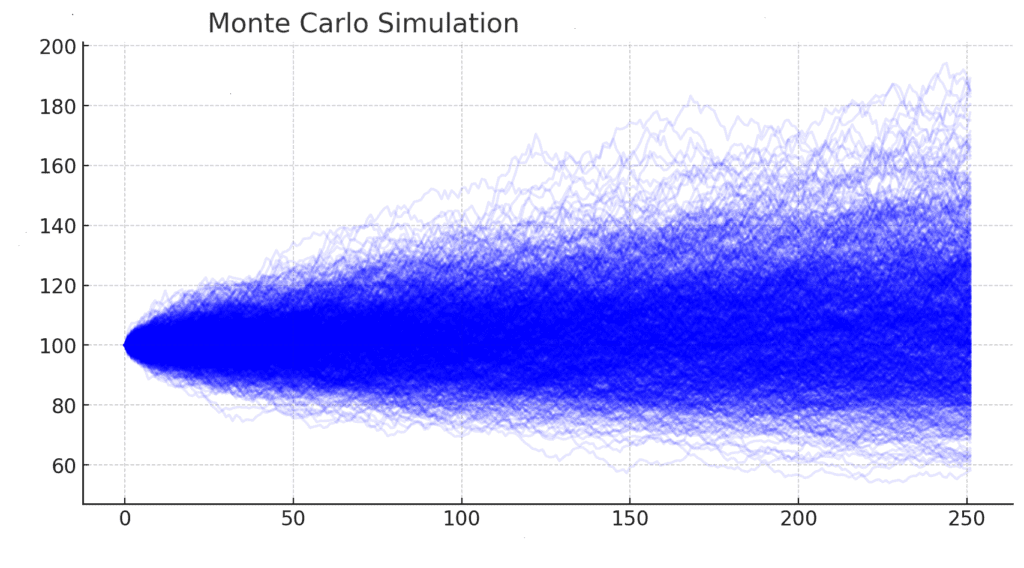
Simulazione Monte Carlo nella modellazione finanziaria: come prevedere rischi e rendimenti
Nel mondo della finanza, l'incertezza è l'unica certezza. Che siate gestori di portafoglio, analisti finanziari o imprenditori, prevedere i risultati futuri è fondamentale per il processo decisionale. I modelli finanziari tradizionali si basano spesso su approcci deterministici, che presuppongono input e output fissi.
Tuttavia, il mondo reale è molto più complesso, con innumerevoli variabili che influenzano i risultati. È qui che Simulazione Monte Carlo entra in gioco: uno strumento potente che consente di modellare l'incertezza e la variabilità insite nei sistemi finanziari.
Che cos'è la simulazione Monte Carlo?
La simulazione Monte Carlo è una tecnica statistica che utilizza il campionamento casuale e la modellazione statistica per stimare funzioni matematiche e simulare il funzionamento di sistemi complessi. Prendendo il nome dal famoso Casinò di Monte Carlo per la sua intrinseca casualità e casualità, questo metodo è diventato un pilastro della modellazione finanziaria.
L'essenza della simulazione Monte Carlo
In sostanza, la simulazione Monte Carlo genera numerosi scenari possibili per un dato processo, ciascuno basato su input casuali. Analizzando i risultati di questi scenari, è possibile ottenere una comprensione probabilistica del comportamento del sistema. Questo è particolarmente utile in finanza, dove variabili come rendimenti di mercato, tassi di interesse e indicatori economici sono incerte.
Contesto storico
Il metodo Monte Carlo fu introdotto per la prima volta in ambito finanziario nel 1964 da David B. Hertz attraverso il suo articolo sulla Harvard Business Review, che ne discuteva l'applicazione alla finanza aziendale. Nel 1977, Phelim Boyle sviluppò la simulazione nella valutazione dei derivati nel suo fondamentale articolo sul Journal of Financial Economics.
Perché utilizzare la simulazione Monte Carlo nella modellazione finanziaria?
Le simulazioni Monte Carlo trovano un ampio spettro di applicazioni in ambito finanziario, aiutando a valutare vari strumenti finanziari e strategie di investimento.
1. Valutazione del portafoglio
Gli investitori utilizzano le simulazioni Monte Carlo per valutare la potenziale performance futura dei loro portafogli di investimento. Le simulazioni possono proiettare i possibili valori del portafoglio nel tempo modellando l'andamento casuale dei prezzi degli asset e le loro correlazioni. Questo aiuta a comprendere la probabilità di raggiungere specifici obiettivi finanziari e a prendere decisioni di investimento consapevoli.
2. Valutazione del rischio
La gestione del rischio è fondamentale in finanza. Le simulazioni Monte Carlo consentono agli analisti di quantificare l'impatto del rischio e dell'incertezza nei modelli finanziari. Gli analisti possono stimare la probabilità di diversi esiti avversi simulando diversi fattori di rischio, come condizioni di mercato, tassi di interesse e indicatori economici, e sviluppare strategie per mitigare potenziali perdite.
3. Prezzo delle opzioni
La valutazione di derivati finanziari complessi, in particolare le opzioni, può essere complessa a causa della loro natura path-dependent. I metodi Monte Carlo sono ampiamente utilizzati per prezzare questi derivati, simulando i numerosi percorsi che il prezzo del sottostante potrebbe seguire e calcolando i relativi payoff. Questo approccio è particolarmente utile per prezzare opzioni esotiche prive di soluzioni in forma chiusa.
4. Budget di capitale e finanza di progetto
Nella finanza aziendale, le simulazioni Monte Carlo vengono utilizzate per valutare la fattibilità di progetti di grandi dimensioni. Modellando le incertezze nei flussi di cassa, nei tassi di sconto e in altre variabili, le aziende possono stimare la distribuzione di probabilità del valore attuale netto (VAN) o del tasso interno di rendimento (TIR) di un progetto. Questa analisi probabilistica contribuisce a prendere decisioni informate in materia di budget di capitale.
Come funziona la simulazione Monte Carlo: una guida passo passo
Analizziamo nel dettaglio il processo di esecuzione di una simulazione Monte Carlo nella modellazione finanziaria:
- Fase 1: definire il problema e identificare le variabili: Inizia definendo chiaramente il problema che vuoi risolvere. Identifica le variabili di input chiave che influenzano il risultato. Ad esempio, se stai modellando i rendimenti azionari, le variabili potrebbero includere il rendimento atteso, la volatilità e l'orizzonte temporale.
- Passaggio 2: specificare le distribuzioni di probabilità: Assegnare distribuzioni di probabilità a ciascuna variabile di input. Le distribuzioni più comuni includono:
- Distribuzione normale: Per variabili come i rendimenti azionari.
- Distribuzione lognormale: Per variabili che non possono essere negative, come i prezzi delle azioni.
- Distribuzione uniforme: Quando tutti i risultati hanno la stessa probabilità.
- Fase 3: Generazione di campioni casuali: Utilizzare un generatore di numeri casuali per creare migliaia o milioni di campioni casuali per ciascuna variabile di input in base alle relative distribuzioni specificate.
- Fase 4: Eseguire le simulazioni: Calcola il risultato utilizzando il tuo modello finanziario per ogni insieme di campioni casuali. Ad esempio, se stai modellando i rendimenti di un portafoglio, potresti usare la formula:

- Fase 5: Analizzare i risultati: Compilare i risultati di tutte le simulazioni per creare una distribuzione di probabilità dei risultati. Analizzare parametri chiave come media, mediana, deviazione standard e percentili.
- Fase 6: Interpretare e prendere decisioni: Utilizza i risultati per valutare il rischio, identificare potenziali risultati e prendere decisioni consapevoli. Ad esempio, potresti determinare la probabilità di raggiungere un rendimento obiettivo o la probabilità di uno scenario peggiore.
Esempio: simulazione Monte Carlo per i rendimenti del portafoglio
Consideriamo un semplice esempio di un portafoglio composto da due asset: Azione A e Azione B. Vogliamo simulare i rendimenti futuri di questo portafoglio in un orizzonte temporale specifico, diciamo 10 anni, utilizzando la simulazione Monte Carlo.
Fase 1: definire il portafoglio
- Azione A: Rendimento annuo previsto = 8%, deviazione standard = 15%
- Azione B: Rendimento annuo previsto = 12%, deviazione standard = 20%
- Correlazione tra il titolo A e il titolo B: 0.5
- Pesi del portafoglio: 60% in magazzino A e 40% in magazzino B
Passaggio 2: generare rendimenti casuali
Genereremo rendimenti casuali per le azioni A e B in base ai loro rendimenti attesi, deviazioni standarde correlazione. Possiamo utilizzare una distribuzione normale multivariata per generare rendimenti casuali correlati.
Fase 3: simulare la crescita del portafoglio
Possiamo simulare la crescita del portafoglio nell'arco di 10 anni capitalizzando i rendimenti annuali.
Fase 4: analizzare i risultati
Dopo aver eseguito la simulazione, possiamo analizzare i risultati per comprendere la distribuzione dei possibili valori del portafoglio dopo 10 anni.
Fase 5: Interpretare i risultati
- Valore medio finale del portafoglio: Valore medio del portafoglio dopo 10 anni in tutte le simulazioni.
- Valore finale mediano del portafoglio: Il valore medio del portafoglio dopo 10 anni, che può essere meno influenzato da risultati estremi.
- Deviazione standard: Misura della dispersione dei valori finali del portafoglio, che indica il rischio associato al portafoglio.
Superare le sfide nella simulazione di Monte Carlo
Sebbene la simulazione Monte Carlo sia uno strumento potente per la modellazione finanziaria, presenta sfide specifiche che i professionisti devono affrontare per garantire risultati accurati e significativi.
1. Scelta delle giuste distribuzioni di probabilità
Selezionare distribuzioni di probabilità appropriate per le variabili di input è fondamentale. Un errore comune è presumere una distribuzione normale per tutte le variabili finanziarie, il che potrebbe non essere sempre accurato. Ad esempio:
- Rendimenti azionari: Spesso modellato utilizzando una distribuzione log-normale anziché una normale, poiché i prezzi delle azioni non possono essere negativi.
- tassi di interesse: Può seguire un processo di inversione della media come il modello di Ornstein-Uhlenbeck.
- prezzi delle materie prime Spesso presentano asimmetria e curtosi, rendendo problematiche le ipotesi sulla distribuzione standard.
Mancia: Utilizzare dati storici e analisi statistiche per determinare la distribuzione più adatta per ciascuna variabile.
2. Gestione delle correlazioni tra variabili
Le variabili finanziarie sono spesso interdipendenti. Ignorare le correlazioni può portare a risultati fuorvianti. Ad esempio, i rendimenti azionari e i tassi di interesse mostrano solitamente relazioni inverse.
Soluzione:
- Utilizzare un matrice di correlazione per modellare le dipendenze tra variabili.
- Impiegare Decomposizione di Cholesky per generare variabili casuali correlate nella simulazione.
3. Complessità computazionale e prestazioni
Le simulazioni Monte Carlo richiedono l'esecuzione di migliaia o addirittura milioni di iterazioni, il che può risultare molto dispendioso in termini di elaborazione dati.
Ottimizzazioni:
- Utilizzo tecniche di riduzione della varianza ad esempio varianti antitetiche O campionamento di importanza per migliorare l'efficienza.
- Parallelizzare i calcoli utilizzando Python multielaborazione o di Excel macro VBA.
4. Interpretazione corretta dei risultati
Una delle insidie più grandi è interpretare male i risultati. Solo perché un particolare scenario ha una bassa probabilità non significa che non si verificherà.
Buone pratiche:
- Guarda il rischio di coda (ad esempio, 5% scenario peggiore) invece di concentrarsi esclusivamente sulla media o sulla mediana.
- Considera di correre test di stress per vedere come si comporta il modello in condizioni estreme.
Come eseguire una simulazione Monte Carlo in Excel e Python
Utilizzando funzioni e strumenti specializzati, le simulazioni Monte Carlo possono essere implementate in Eccellere E Pitone.
1. Simulazione Monte Carlo in Excel
Excel è uno strumento eccellente per simulazioni Monte Carlo rapide e accessibili.
Passaggi:
- Definire il modello
- Scegliere una formula o un processo con variabili incerte (ad esempio, prevedere i prezzi delle azioni o i costi del progetto).
- Variabili casuali di input
- Utilizzare =RAND() per numeri casuali uniformi compresi tra 0 e 1.
- Utilizzare =NORM.INV(RAND(), media, dev_std) per valori distribuiti normalmente.
- Simulare più scenari
- Trascina la formula verso il basso per generare migliaia di scenari casuali.
- Calcola le statistiche chiave
- Calcola la media, la deviazione standard e altre metriche rilevanti utilizzando le funzioni di Excel.
- Analizza i risultati con gli istogrammi
- Utilizzare Excel Strumento di analisi dei dati per creare un istogramma.
Esempio: Simulazione del prezzo delle azioni
Supponiamo che il rendimento atteso di un titolo sia 7% con un Deviazione standard 15% oltre un anno.
- Nella cella A1, inserisci il prezzo iniziale: 100
- In B1, inserisci la formula per il prezzo dell'anno successivo
- Trascina questa formula verso il basso simulare 1000 scenari.
- Calcolare:
- Prezzo medio: =MEDIA(B1:B1000)
- Deviazione standard: =DEV.ST(B1:B1000)
2. Simulazione Monte Carlo in Python
Python fornisce un modo più robusto e flessibile per eseguire simulazioni Monte Carlo utilizzando NumPy, Pandas e Matplotlib.
Esempio: Simulazione del prezzo delle azioni
Quando usare Excel o Python
| Caratteristica | Eccellere | Pitone |
| Facilità d'uso | Semplice per modelli su piccola scala | Meglio per simulazioni su larga scala |
| Prestazione | Più lento con set di dati di grandi dimensioni | Più veloce ed efficiente |
| Flessibilità | Funzioni statistiche limitate | Maggiore personalizzazione (NumPy, SciPy) |
| Visualizzazione | Grafici di base | Tracciamento avanzato (Matplotlib, Seaborn) |
Suggerimenti pratici per una simulazione Monte Carlo efficace
- Inizia in modo semplice: Inizia con un modello base e aggiungi gradualmente complessità man mano che acquisisci sicurezza.
- Convalida gli input: Assicurati che le variabili di input e le distribuzioni siano realistiche e basate su dati affidabili.
- Eseguire sufficienti simulazioni: L'accuratezza dei risultati dipende dal numero di simulazioni. L'obiettivo è di almeno 10.000 iterazioni.
- Utilizzare l'analisi di sensibilità: Identificare quali variabili hanno un impatto più significativo sui risultati.
- Ipotesi del documento: Documenta tutte le ipotesi e le limitazioni del tuo modello.
Caso di studio: simulazione Monte Carlo nella valutazione del progetto utilizzando un modello finanziario
In questo caso di studio, valuteremo un ipotetico progetto infrastrutturale utilizzando la simulazione di Monte Carlo per stimare l' Valore attuale netto (VAN), considerando l'incertezza nei parametri finanziari chiave come investimento iniziale, crescita del fatturato, costi operativi e tasso di sconto.
Panoramica del progetto
- Nome del progetto: Impianto di energia verde
- Durata del progetto: 10 anni
- Investimento iniziale: $50 milioni
- Tasso di crescita annuale dei ricavi: 5% (±2%)
- Costi operativi: 30% di entrate (±5%)
- Tasso di sconto: 8% (±1%)
La simulazione Monte Carlo aiuterà ad analizzare la gamma dei possibili VAN, fornendo informazioni sulla fattibilità finanziaria del progetto in diversi scenari.
Configurazione della simulazione Monte Carlo
Per eseguire la simulazione:
- Definire le distribuzioni di probabilità per i principali input finanziari:
- Tasso di crescita dei ricavi: Distribuzione normale (media = 5%, deviazione standard = 2%)
- Costi operativi pari a % di ricavi: Distribuzione normale (media = 30%, deviazione standard = 5%)
- Tasso di sconto: Distribuzione normale (media = 8%, deviazione standard = 1%)
- Esegui 10.000 simulazioni, calcolando il VAN per ogni esecuzione.
- Riepilogare i risultati utilizzando misure statistiche e visualizzazioni.
Adesso eseguirò la simulazione Monte Carlo e genererò i risultati.
Simulazione Monte Carlo: distribuzione del VAN
Risultati della simulazione di Monte Carlo
| Tasso di crescita | Costo operativo % | Tasso di sconto | |
| contare | 10000.0 | 10000.0 | 10000.0 |
| Significare | 0.050040570362915315 | 0.3002260181128686 | 0.07997808603004744 |
| standard | 0.019910554247468792 | 0.04968107384600725 | 0.01008925573859806 |
| minimo | -0.01856183610533345 | 0.11544796696907525 | 0.04046458542990874 |
| 25% | 0.03640861533085948 | 0.26678017932445197 | 0.07319111966613821 |
I risultati della simulazione Monte Carlo sono ora disponibili. L'istogramma mostra la distribuzione dei risultati del Valore Attuale Netto (VAN), evidenziando l'incertezza finanziaria del progetto. È inoltre possibile esplorare la tabella delle statistiche di riepilogo per esaminare informazioni chiave, come media, deviazione standard e valori percentili per VAN, tasso di crescita, costi operativi e tasso di sconto. Fatemi sapere se avete bisogno di ulteriori analisi o interpretazioni!
Conclusione: perché la simulazione Monte Carlo è un punto di svolta
La simulazione di Monte Carlo è uno degli strumenti più efficaci per la valutazione del rischio e le previsioni finanziarieA differenza dei modelli statici tradizionali, fornisce un visione probabilistica dei potenziali risultati, aiutando investitori e aziende a prendere decisioni basate sui dati.
Per semplificare le simulazioni Monte Carlo e migliorare la precisione, SHEETS.MARKET offre modelli professionali che ti consentono di:
- Esegui migliaia di simulazioni con pochi clic.
- Visualizzare le distribuzioni del rischio immediatamente.
- Personalizza i modelli per le tue esigenze finanziarie.
🚀 Risparmia tempo e migliora la precisione: esplora Fogli.Mercato per strumenti di modellazione finanziaria da esperti oggi stesso! Per ulteriori approfondimenti sulla modellazione finanziaria, l'analisi del rischio e le simulazioni Monte Carlo, seguici su LinkedInPartecipa alla conversazione e scopri come questi strumenti possono supportare il tuo processo decisionale.