Modèles financiers
Simulation de Monte-Carlo dans la modélisation financière : comment prédire les risques et les rendements
Dans le monde de la finance, l'incertitude est la seule certitude. Que vous soyez gestionnaire de portefeuille, analyste financier ou chef d'entreprise, prédire les résultats futurs est un élément essentiel de la prise de décision. Les modèles financiers traditionnels s'appuient souvent sur des approches déterministes, qui supposent des entrées et des sorties fixes.
Cependant, le monde réel est bien plus complexe, avec d'innombrables variables influençant les résultats. C'est là que Simulation de Monte Carlo entre en jeu : un outil puissant qui vous permet de modéliser l’incertitude et la variabilité inhérentes aux systèmes financiers.
Qu'est-ce que la simulation de Monte Carlo ?
La simulation de Monte-Carlo est une technique statistique qui utilise l'échantillonnage aléatoire et la modélisation statistique pour estimer des fonctions mathématiques et reproduire le fonctionnement de systèmes complexes. Nommée d'après le célèbre casino de Monte-Carlo en raison de son caractère aléatoire et aléatoire, cette méthode est devenue un élément fondamental de la modélisation financière.
L'essence de la simulation de Monte Carlo
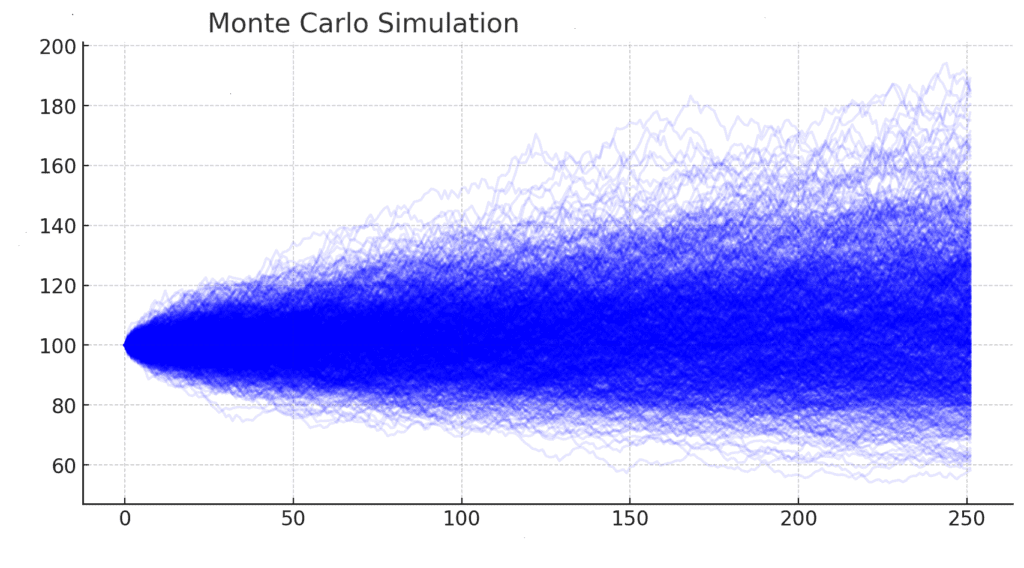
Fondamentalement, la simulation de Monte-Carlo génère de nombreux scénarios possibles pour un processus donné, chacun basé sur des données aléatoires. L'analyse des résultats de ces scénarios permet d'obtenir une compréhension probabiliste du comportement du système. Ceci est particulièrement utile en finance, où des variables telles que les rendements du marché, les taux d'intérêt et les indicateurs économiques sont incertaines.
Contexte historique
La méthode de Monte-Carlo a été introduite pour la première fois en finance en 1964 par David B. Hertz dans un article paru dans la Harvard Business Review, qui traitait de son application à la finance d'entreprise. En 1977, Phelim Boyle a été le pionnier de la simulation pour l'évaluation des produits dérivés dans son article fondateur paru dans le Journal of Financial Economics.
Pourquoi utiliser la simulation de Monte Carlo dans la modélisation financière ?
Les simulations de Monte Carlo ont un large spectre d’applications en finance, aidant à évaluer divers instruments financiers et stratégies d’investissement.
1. Évaluation du portefeuille
Les investisseurs utilisent les simulations de Monte-Carlo pour évaluer la performance future potentielle de leurs portefeuilles d'investissement. Ces simulations permettent de projeter la valeur potentielle d'un portefeuille au fil du temps en modélisant le comportement aléatoire des prix des actifs et leurs corrélations. Cela permet de comprendre la probabilité d'atteindre des objectifs financiers spécifiques et de prendre des décisions d'investissement éclairées.
2. Évaluation des risques
La gestion des risques est primordiale en finance. Les simulations de Monte-Carlo permettent aux analystes de quantifier l'impact du risque et de l'incertitude dans les modèles financiers. Ils peuvent estimer la probabilité de différents résultats défavorables en simulant divers facteurs de risque, tels que les conditions de marché, les taux d'intérêt et les indicateurs économiques, et élaborer des stratégies pour atténuer les pertes potentielles.
3. Tarification des options
L'évaluation de produits dérivés financiers complexes, notamment d'options, peut s'avérer complexe en raison de leur nature dépendante du chemin parcouru. Les méthodes de Monte-Carlo sont largement utilisées pour évaluer ces produits dérivés en simulant les multiples trajectoires possibles du prix de l'actif sous-jacent et en calculant les gains correspondants. Cette approche est particulièrement utile pour évaluer les options exotiques dépourvues de solutions fermées.
4. Budgétisation des investissements et financement des projets
En finance d'entreprise, les simulations de Monte-Carlo sont utilisées pour évaluer la viabilité des grands projets. En modélisant les incertitudes liées aux flux de trésorerie, aux taux d'actualisation et à d'autres variables, les entreprises peuvent estimer la distribution de probabilité de la valeur actuelle nette (VAN) ou du taux de rentabilité interne (TRI) d'un projet. Cette approche probabiliste facilite la prise de décisions éclairées en matière de budgétisation des investissements.
Comment fonctionne la simulation de Monte-Carlo : un guide étape par étape
Décomposons le processus de réalisation d’une simulation de Monte Carlo dans la modélisation financière :
- Étape 1 : Définir le problème et identifier les variables : Commencez par définir clairement le problème que vous souhaitez résoudre. Identifiez les variables d'entrée clés qui influencent le résultat. Par exemple, si vous modélisez le rendement d'une action, les variables peuvent inclure le rendement attendu, la volatilité et l'horizon temporel.
- Étape 2 : Spécifier les distributions de probabilité : Attribuez des distributions de probabilité à chaque variable d'entrée. Les distributions courantes incluent :
- Distribution normale:Pour des variables telles que les rendements boursiers.
- Distribution log-normale:Pour les variables qui ne peuvent pas être négatives, comme les cours des actions.
- Distribution uniforme:Lorsque tous les résultats sont également probables.
- Étape 3 : Générer des échantillons aléatoires : Utilisez un générateur de nombres aléatoires pour créer des milliers ou des millions d’échantillons aléatoires pour chaque variable d’entrée en fonction de leurs distributions spécifiées.
- Étape 4 : Exécuter les simulations : Calculez le résultat à l'aide de votre modèle financier pour chaque ensemble d'échantillons aléatoires. Par exemple, si vous modélisez le rendement d'un portefeuille, vous pouvez utiliser la formule suivante :

- Étape 5 : Analyser les résultats : Compilez les résultats de toutes les simulations pour créer une distribution de probabilité des résultats. Analysez les indicateurs clés tels que la moyenne, la médiane, l'écart type et les percentiles.
- Étape 6 : Interpréter et prendre des décisions : Utilisez les résultats pour évaluer les risques, identifier les résultats potentiels et prendre des décisions éclairées. Par exemple, vous pouvez déterminer la probabilité d'atteindre un rendement cible ou la probabilité d'un scénario catastrophe.
Exemple : Simulation de Monte-Carlo pour les rendements de portefeuille
Considérons un exemple simple d'un portefeuille composé de deux actifs : l'action A et l'action B. Nous voulons simuler les rendements futurs de ce portefeuille sur un horizon temporel spécifique, disons 10 ans, en utilisant la simulation de Monte Carlo.
Étape 1 : Définir le portefeuille
- Action A:Rendement annuel attendu = 8%, Écart type = 15%
- Stock B: Rendement annuel attendu = 12%, Écart type = 20%
- Corrélation entre l'action A et l'action B: 0.5
- Pondérations du portefeuille: 60% en stock A et 40% en stock B
Étape 2 : générer des retours aléatoires
Nous générerons des rendements aléatoires pour les actions A et B en fonction de leurs rendements attendus, écarts typeset corrélation. Nous pouvons utiliser une distribution normale multivariée pour générer des rendements aléatoires corrélés.
Étape 3 : Simuler la croissance du portefeuille
Nous pouvons simuler la croissance du portefeuille sur 10 ans en capitalisant les rendements annuels.
Étape 4 : Analyser les résultats
Après avoir exécuté la simulation, nous pouvons analyser les résultats pour comprendre la distribution des valeurs possibles du portefeuille après 10 ans.
Étape 5 : Interpréter les résultats
- Valeur finale moyenne du portefeuille:La valeur moyenne du portefeuille après 10 ans sur toutes les simulations.
- Valeur médiane finale du portefeuille:La valeur moyenne du portefeuille après 10 ans, qui peut être moins affectée par des résultats extrêmes.
- Écart type:Une mesure de la dispersion des valeurs finales du portefeuille, indiquant le risque associé au portefeuille.
Surmonter les défis de la simulation de Monte Carlo
Bien que la simulation de Monte Carlo soit un outil puissant pour la modélisation financière, elle comporte des défis spécifiques que les professionnels doivent relever pour garantir des résultats précis et significatifs.
1. Choisir les bonnes distributions de probabilité
Il est crucial de sélectionner des distributions de probabilité appropriées pour les variables d'entrée. Une erreur courante consiste à supposer une distribution normale pour toutes les variables financières, ce qui n'est pas toujours exact. Par exemple :
- Rendements des actions:Souvent modélisé à l'aide d'une distribution log-normale plutôt que normale, car les cours des actions ne peuvent pas être négatifs.
- Taux d'intérêt:Peut suivre un processus de retour à la moyenne tel que le modèle d'Ornstein-Uhlenbeck.
- prix des matières premières Ils présentent souvent une asymétrie et une courbure, ce qui rend les hypothèses de distribution standard problématiques.
Conseil: Utilisez des données historiques et des analyses statistiques pour déterminer la distribution la plus adaptée à chaque variable.
2. Gestion des corrélations entre les variables
Les variables financières sont souvent interdépendantes. Ignorer les corrélations peut conduire à des résultats trompeurs. Par exemple, les rendements boursiers et les taux d'intérêt présentent généralement des relations inverses.
Solution:
- Utiliser un matrice de corrélation pour modéliser les dépendances entre les variables.
- Employer Décomposition de Cholesky pour générer des variables aléatoires corrélées dans la simulation.
3. Complexité et performances informatiques
Les simulations de Monte Carlo nécessitent l’exécution de milliers, voire de millions d’itérations, ce qui peut nécessiter beaucoup de calculs.
Optimisations :
- Utiliser techniques de réduction de la variance tel que variantes antithétiques ou échantillonnage d'importance pour améliorer l'efficacité.
- Paralléliser les calculs à l'aide de Python multitraitement ou Excel Macros VBA.
4. Interpréter correctement les résultats
L'un des plus grands pièges est de mal interpréter les résultats. Ce n'est pas parce qu'un scénario particulier est peu probable qu'il ne se produira pas.
Meilleures pratiques :
- Regardez le risque extrême (par exemple, le pire scénario 5%) au lieu de se concentrer uniquement sur la moyenne ou la médiane.
- Envisagez de courir tests de résistance pour voir comment le modèle se comporte dans des conditions extrêmes.
Comment effectuer une simulation de Monte Carlo dans Excel et Python
En utilisant des fonctions et des outils spécialisés, les simulations de Monte Carlo peuvent être mises en œuvre dans Exceller et Python.
1. Simulation de Monte Carlo dans Excel
Excel est un excellent outil pour des simulations Monte Carlo rapides et accessibles.
Mesures:
- Définir le modèle
- Choisissez une formule ou un processus avec des variables incertaines (par exemple, prédire les cours des actions ou les coûts du projet).
- Variables aléatoires d'entrée
- Utilisez =RAND() pour les nombres aléatoires uniformes compris entre 0 et 1.
- Utilisez =NORM.INV(RAND(), mean, std_dev) pour les valeurs distribuées normalement.
- Simuler plusieurs scénarios
- Faites glisser la formule vers le bas pour générer des milliers de scénarios aléatoires.
- Calculer les statistiques clés
- Calculez la moyenne, l’écart type et d’autres mesures pertinentes à l’aide des fonctions Excel.
- Analyser les résultats avec des histogrammes
- Utiliser Excel Pack d'outils d'analyse de données pour créer un histogramme.
Exemple : Simulation du cours des actions
Supposons que le rendement attendu d'une action soit 7% avec un Écart type 15% plus d'un an.
- En cellule A1, entrez le prix de départ : 100
- Dans B1, entrez la formule pour le prix de l'année suivante
- Faites glisser cette formule vers le bas pour simuler 1000 scénarios.
- Calculer:
- Prix moyen: =MOYENNE(B1:B1000)
- Écart type: =ÉCART-TYPE(B1:B1000)
2. Simulation de Monte Carlo en Python
Python fournit un moyen plus robuste et plus flexible d'exécuter des simulations Monte Carlo à l'aide de NumPy, Pandas et Matplotlib.
Exemple : Simulation du cours des actions
Quand utiliser Excel ou Python
| Fonctionnalité | Exceller | Python |
| Facilité d'utilisation | Simple pour les modèles à petite échelle | Idéal pour les simulations à grande échelle |
| Performance | Plus lent avec de grands ensembles de données | Plus rapide et plus efficace |
| Flexibilité | Fonctions statistiques limitées | Plus de personnalisation (NumPy, SciPy) |
| Visualisation | Cartes de base | Tracé avancé (Matplotlib, Seaborn) |
Conseils pratiques pour une simulation Monte Carlo efficace
- Commencez simplement:Commencez par un modèle de base et ajoutez progressivement de la complexité à mesure que vous gagnez en confiance.
- Valider les entrées: Assurez-vous que vos variables d’entrée et vos distributions sont réalistes et basées sur des données fiables.
- Exécutez suffisamment de simulations:La précision de vos résultats dépend du nombre de simulations. Visez au moins 10 000 itérations.
- Utiliser l'analyse de sensibilité: Identifiez les variables qui ont le plus d’impact sur les résultats.
- Hypothèses du document:Documentez toutes les hypothèses et limites de votre modèle.
Étude de cas : Simulation de Monte-Carlo dans l'évaluation de projets à l'aide d'un modèle financier
Dans cette étude de cas, nous évaluerons un projet d'infrastructure hypothétique en utilisant la simulation de Monte Carlo pour estimer le Valeur actuelle nette (VAN), compte tenu de l’incertitude des paramètres financiers clés tels que investissement initial, croissance des revenus, coûts d'exploitation et taux d'actualisation.
Aperçu du projet
- Nom du projet: Centrale d'énergie verte
- Durée du projet: 10 ans
- Investissement initial: $50 millions
- Taux de croissance annuel des revenus: 5% (±2%)
- Coûts d'exploitation: 30% de revenus (±5%)
- Taux d'actualisation: 8% (±1%)
La simulation de Monte Carlo aidera à analyser la gamme des VAN possibles, fournissant des informations sur la viabilité financière du projet dans différents scénarios.
Configuration de simulation de Monte Carlo
Pour réaliser la simulation :
- Définir les distributions de probabilité pour les apports financiers clés :
- Taux de croissance des revenus: Distribution normale (moyenne = 5%, écart type = 2%)
- Coûts d'exploitation représentant % de revenus: Distribution normale (moyenne = 30%, écart type = 5%)
- Taux d'actualisation: Distribution normale (moyenne = 8%, écart type = 1%)
- Exécutez 10 000 simulations, calculant la VAN pour chaque exécution.
- Résumer les résultats en utilisant des mesures statistiques et des visualisations.
Maintenant, je vais exécuter la simulation de Monte Carlo et générer les résultats.
Simulation de Monte-Carlo : distribution de la VAN
Résultats de la simulation de Monte Carlo
| Taux de croissance | Coût d'exploitation % | Taux d'actualisation | |
| compter | 10000.0 | 10000.0 | 10000.0 |
| signifier | 0.050040570362915315 | 0.3002260181128686 | 0.07997808603004744 |
| MST | 0.019910554247468792 | 0.04968107384600725 | 0.01008925573859806 |
| min | -0.01856183610533345 | 0.11544796696907525 | 0.04046458542990874 |
| 25% | 0.03640861533085948 | 0.26678017932445197 | 0.07319111966613821 |
Les résultats de la simulation de Monte-Carlo sont désormais disponibles. L'histogramme présente la distribution des résultats de la valeur actuelle nette (VAN), soulignant l'incertitude financière du projet. Vous pouvez également consulter le tableau récapitulatif des statistiques pour consulter des informations clés, telles que la moyenne, l'écart type et les valeurs en percentile de la VAN, du taux de croissance, des coûts d'exploitation et du taux d'actualisation. N'hésitez pas à me contacter pour toute analyse ou interprétation complémentaire !
Conclusion : Pourquoi la simulation de Monte-Carlo change la donne
La simulation de Monte Carlo est l'un des outils les plus efficaces pour l'évaluation des risques et les prévisions financièresContrairement aux modèles statiques traditionnels, il fournit une vision probabiliste des résultats potentiels, aidant les investisseurs et les entreprises à prendre des décisions fondées sur les données.
Pour simplifier les simulations de Monte Carlo et améliorer la précision, SHEETS.MARKET propose des modèles professionnels qui vous permettent de :
- Exécutez des milliers de simulations en quelques clics seulement.
- Visualiser les distributions de risques immédiatement.
- Personnaliser les modèles pour vos besoins financiers.
🚀 Gagnez du temps et améliorez la précision : explorez Sheets.Market pour des outils de modélisation financière experts dès aujourd'hui ! Pour plus d'informations sur la modélisation financière, l'analyse des risques et les simulations de Monte Carlo, suivez-nous sur LinkedInRejoignez la conversation et découvrez comment ces outils peuvent soutenir votre processus de prise de décision.