Modelos financieros
Simulación de Monte Carlo en el modelado financiero: Cómo predecir el riesgo y la rentabilidad
En el mundo de las finanzas, la incertidumbre es la única certeza. Ya seas gestor de cartera, analista financiero o empresario, predecir resultados futuros es fundamental para la toma de decisiones. Los modelos financieros tradicionales suelen basarse en enfoques deterministas, que asumen entradas y salidas fijas.
Sin embargo, el mundo real es mucho más complejo, con innumerables variables que influyen en los resultados. Aquí es donde Simulación de Monte Carlo Entra en juego una herramienta poderosa que permite modelar la incertidumbre y la variabilidad inherentes a los sistemas financieros.
¿Qué es la simulación de Monte Carlo?
La simulación de Monte Carlo es una técnica estadística que utiliza muestreo aleatorio y modelado estadístico para estimar funciones matemáticas e imitar el funcionamiento de sistemas complejos. Nombrado en honor al famoso Casino de Monte Carlo debido a su inherente aleatoriedad y azar, este método se ha convertido en una pieza clave en el modelado financiero.
La esencia de la simulación de Monte Carlo
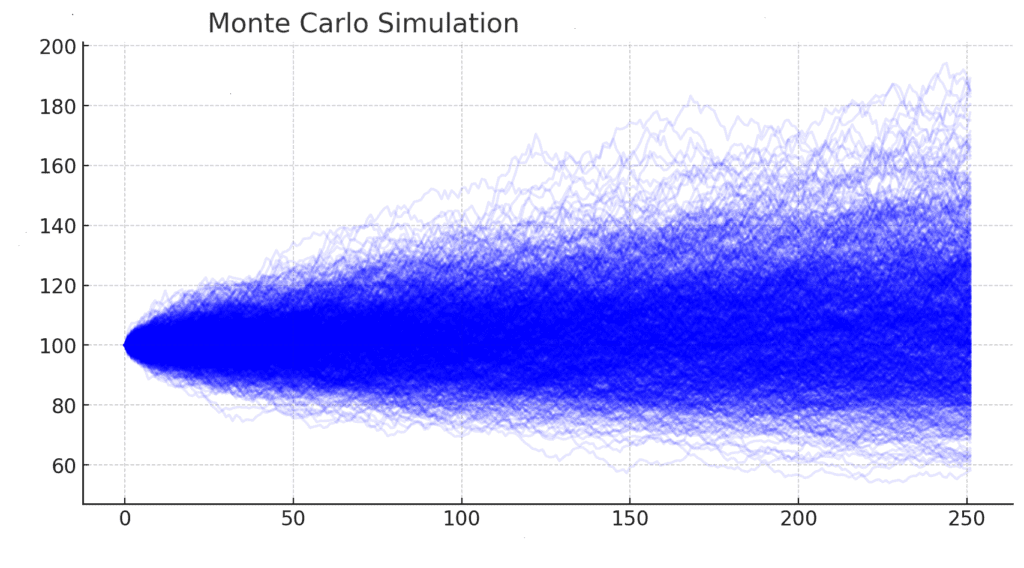
En esencia, la simulación de Monte Carlo genera numerosos escenarios posibles para un proceso dado, cada uno basado en entradas aleatorias. Al analizar los resultados de estos escenarios, se puede obtener una comprensión probabilística del comportamiento del sistema. Esto es particularmente útil en finanzas, donde variables como la rentabilidad del mercado, las tasas de interés y los indicadores económicos son inciertas.
Contexto histórico
El método de Monte Carlo fue introducido por primera vez en las finanzas en 1964 por David B. Hertz en su artículo de Harvard Business Review, donde analizaba su aplicación en finanzas corporativas. En 1977, Phelim Boyle fue pionero en la simulación de la valoración de derivados en su influyente artículo publicado en el Journal of Financial Economics.
¿Por qué utilizar la simulación de Monte Carlo en el modelado financiero?
Las simulaciones de Monte Carlo tienen un amplio espectro de aplicaciones en finanzas y ayudan a evaluar diversos instrumentos financieros y estrategias de inversión.
1. Valoración de cartera
Los inversores utilizan simulaciones de Monte Carlo para evaluar el rendimiento futuro potencial de sus carteras de inversión. Las simulaciones pueden proyectar posibles valores de la cartera a lo largo del tiempo modelando el comportamiento aleatorio de los precios de los activos y sus correlaciones. Esto ayuda a comprender la probabilidad de alcanzar objetivos financieros específicos y a tomar decisiones de inversión informadas.
2. Evaluación de riesgos
La gestión de riesgos es fundamental en finanzas. Las simulaciones de Monte Carlo permiten a los analistas cuantificar el impacto del riesgo y la incertidumbre en los modelos financieros. Los analistas pueden estimar la probabilidad de diferentes resultados adversos mediante la simulación de diversos factores de riesgo, como las condiciones del mercado, los tipos de interés y los indicadores económicos, y desarrollar estrategias para mitigar posibles pérdidas.
3. Precio de las opciones
La valoración de derivados financieros complejos, en particular las opciones, puede ser compleja debido a su naturaleza dependiente de la trayectoria. Los métodos de Monte Carlo se utilizan ampliamente para fijar el precio de estos derivados, simulando las numerosas trayectorias que podría tomar el precio del activo subyacente y calculando las correspondientes rentabilidades. Este enfoque es especialmente beneficioso para la valoración de opciones exóticas que carecen de soluciones cerradas.
4. Presupuesto de capital y financiación de proyectos
En finanzas corporativas, las simulaciones de Monte Carlo se emplean para evaluar la viabilidad de grandes proyectos. Al modelar las incertidumbres en los flujos de caja, las tasas de descuento y otras variables, las empresas pueden estimar la distribución de probabilidad del valor actual neto (VAN) o la tasa interna de retorno (TIR) de un proyecto. Esta perspectiva probabilística facilita la toma de decisiones informadas sobre la presupuestación de capital.
Cómo funciona la simulación de Monte Carlo: una guía paso a paso
Analicemos el proceso de realización de una simulación de Monte Carlo en el modelado financiero:
- Paso 1: Definir el problema e identificar las variables: Empiece por definir claramente el problema que desea resolver. Identifique las variables de entrada clave que influyen en el resultado. Por ejemplo, si está modelando la rentabilidad de las acciones, las variables podrían incluir la rentabilidad esperada, la volatilidad y el horizonte temporal.
- Paso 2: Especificar distribuciones de probabilidad: Asignar distribuciones de probabilidad a cada variable de entrada. Las distribuciones comunes incluyen:
- Distribución normal:Para variables como el rendimiento de las acciones.
- Distribución lognormal:Para variables que no pueden ser negativas, como los precios de las acciones.
- Distribución uniforme:Cuando todos los resultados son igualmente probables.
- Paso 3: Generar muestras aleatorias: Utilice un generador de números aleatorios para crear miles o millones de muestras aleatorias para cada variable de entrada en función de sus distribuciones específicas.
- Paso 4: Ejecutar simulaciones: Calcule el resultado utilizando su modelo financiero para cada conjunto de muestras aleatorias. Por ejemplo, si está modelando la rentabilidad de una cartera, podría usar la fórmula:

- Paso 5: Analizar los resultados: Recopile los resultados de todas las simulaciones para crear una distribución de probabilidad de resultados. Analice métricas clave como la media, la mediana, la desviación estándar y los percentiles.
- Paso 6: Interpretar y tomar decisiones: Utilice los resultados para evaluar el riesgo, identificar posibles resultados y tomar decisiones informadas. Por ejemplo, podría determinar la probabilidad de alcanzar una rentabilidad objetivo o la probabilidad de que se produzca el peor escenario posible.
Ejemplo: Simulación de Monte Carlo para la rentabilidad de una cartera
Consideremos un ejemplo simple de una cartera que consta de dos activos: acciones A y acciones B. Queremos simular los rendimientos futuros de esta cartera durante un horizonte temporal específico, digamos 10 años, utilizando la simulación de Monte Carlo.
Paso 1: Definir la cartera
- Acción A:Rendimiento anual esperado = 8%, Desviación estándar = 15%
- Stock B:Rendimiento anual esperado = 12%, Desviación estándar = 20%
- Correlación entre las acciones A y B: 0.5
- Ponderaciones de la cartera:60% en stock A y 40% en stock B
Paso 2: Generar retornos aleatorios
Generaremos rendimientos aleatorios para las acciones A y B en función de sus rendimientos esperados. desviaciones estándary correlación. Podemos utilizar una distribución normal multivariante para generar retornos aleatorios correlacionados.
Paso 3: Simular el crecimiento de la cartera
Podemos simular el crecimiento de la cartera a lo largo de 10 años capitalizando los rendimientos anuales.
Paso 4: Analizar los resultados
Después de ejecutar la simulación, podemos analizar los resultados para comprender la distribución de los posibles valores de la cartera después de 10 años.
Paso 5: Interpretar los resultados
- Valor medio final de la cartera:El valor promedio de la cartera después de 10 años en todas las simulaciones.
- Valor final medio de la cartera:El valor medio de la cartera después de 10 años, que puede verse menos afectado por resultados extremos.
- Desviación estándar:Una medida de la dispersión de los valores finales de la cartera, que indica el riesgo asociado con la cartera.
Superando desafíos en la simulación de Monte Carlo
Si bien la simulación de Monte Carlo es una herramienta poderosa para el modelado financiero, presenta desafíos específicos que los profesionales deben abordar para garantizar resultados precisos y significativos.
1. Cómo elegir las distribuciones de probabilidad correctas
Seleccionar distribuciones de probabilidad adecuadas para las variables de entrada es crucial. Un error común es asumir una distribución normal para todas las variables financieras, lo cual no siempre es preciso. Por ejemplo:
- Rendimiento de las acciones:A menudo se modela utilizando una distribución log-normal en lugar de una normal, ya que los precios de las acciones no pueden ser negativos.
- Tasas de interés:Puede seguir un proceso de reversión a la media como el modelo de Ornstein-Uhlenbeck.
- Precios de las materias primas A menudo presentan asimetría y curtosis, lo que hace que las suposiciones de distribución estándar sean problemáticas.
Consejo: Utilice datos históricos y análisis estadístico para determinar la distribución más adecuada para cada variable.
2. Manejo de correlaciones entre variables
Las variables financieras suelen ser interdependientes. Ignorar las correlaciones puede generar resultados engañosos. Por ejemplo, la rentabilidad de las acciones y las tasas de interés suelen presentar relaciones inversas.
Solución:
- Utilice un matriz de correlación para modelar dependencias entre variables.
- Emplear Descomposición de Cholesky para generar variables aleatorias correlacionadas en la simulación.
3. Complejidad computacional y rendimiento
Las simulaciones de Monte Carlo requieren ejecutar miles o incluso millones de iteraciones, lo que puede resultar computacionalmente intensivo.
Optimizaciones:
- Usar técnicas de reducción de varianza como variantes antitéticas o muestreo de importancia para mejorar la eficiencia.
- Paralelizar cálculos usando Python multiprocesamiento o de Excel Macros de VBA.
4. Interpretación correcta de los resultados
Uno de los mayores obstáculos es malinterpretar los resultados. Que un escenario en particular tenga baja probabilidad no significa que no ocurra.
Mejores prácticas:
- Mira el riesgo de cola (por ejemplo, 5%, el peor escenario posible) en lugar de centrarse únicamente en la media o la mediana.
- Considere correr pruebas de estrés para ver cómo se comporta el modelo en condiciones extremas.
Cómo realizar una simulación de Monte Carlo en Excel y Python
Utilizando funciones y herramientas especializadas, se pueden implementar simulaciones de Monte Carlo en Sobresalir y Pitón.
1. Simulación de Monte Carlo en Excel
Excel es una herramienta excelente para realizar simulaciones de Monte Carlo rápidas y accesibles.
Pasos:
- Definir el modelo
- Decidir sobre una fórmula o proceso con variables inciertas (por ejemplo, predecir los precios de las acciones o los costos del proyecto).
- Variables aleatorias de entrada
- Utilice =RAND() para números aleatorios uniformes entre 0 y 1.
- Utilice =NORM.INV(RAND(), media, desviación estándar) para valores distribuidos normalmente.
- Simular múltiples escenarios
- Arrastre la fórmula hacia abajo para generar miles de escenarios aleatorios.
- Calcular estadísticas clave
- Calcule la media, la desviación estándar y otras métricas relevantes utilizando funciones de Excel.
- Analizar resultados con histogramas
- Utilice Excel Paquete de herramientas de análisis de datos para crear un histograma.
Ejemplo: Simulación del precio de las acciones
Supongamos que el rendimiento esperado de una acción es 7% con un desviación estándar 15% más de un año.
- En la celda A1, introduzca el precio inicial: 100
- En B1, ingrese la fórmula para el precio del próximo año
- Arrastre esta fórmula hacia abajo para simular 1000 escenarios.
- Calcular:
- Precio medio: =PROMEDIO(B1:B1000)
- desviación estándar: =DESVEST(B1:B1000)
2. Simulación de Monte Carlo en Python
Python proporciona una forma más robusta y flexible de ejecutar simulaciones de Monte Carlo utilizando NumPy, Pandas y Matplotlib.
Ejemplo: Simulación del precio de las acciones
Cuándo usar Excel o Python
| Característica | Sobresalir | Pitón |
| Facilidad de uso | Simple para modelos a pequeña escala | Mejor para simulaciones a gran escala |
| Actuación | Más lento con grandes conjuntos de datos | Más rápido y más eficiente |
| Flexibilidad | Funciones estadísticas limitadas | Más personalización (NumPy, SciPy) |
| Visualización | Gráficos básicos | Trazado avanzado (Matplotlib, Seaborn) |
Consejos prácticos para una simulación de Monte Carlo eficaz
- Empieza de forma sencilla:Comience con un modelo básico y agregue complejidad gradualmente a medida que gane confianza.
- Validar entradas:Asegúrese de que sus variables de entrada y distribuciones sean realistas y se basen en datos confiables.
- Ejecute suficientes simulacionesLa precisión de los resultados depende del número de simulaciones. Procura realizar al menos 10 000 iteraciones.
- Utilice el análisis de sensibilidad:Identificar qué variables impactan los resultados de manera más significativa.
- Supuestos del documento:Documente todas las suposiciones y limitaciones de su modelo.
Estudio de caso: Simulación de Monte Carlo en la valoración de proyectos mediante un modelo financiero
En este estudio de caso, evaluaremos un proyecto de infraestructura hipotético utilizando simulación de Monte Carlo para estimar el Valor actual neto (VAN), considerando la incertidumbre en parámetros financieros clave como inversión inicial, crecimiento de los ingresos, costos operativos y tasa de descuento.
Descripción general del proyecto
- Nombre del proyecto: Planta de energía verde
- Duración del proyecto:10 años
- Inversión inicial:$50 millones
- Tasa de crecimiento anual de los ingresos:5% (±2%)
- Costos de operación:30% de ingresos (±5%)
- Tasa de descuento:8% (±1%)
La simulación de Monte Carlo ayudará a analizar el rango de posibles VPN, brindando información sobre la viabilidad financiera del proyecto en diferentes escenarios.
Configuración de simulación de Monte Carlo
Para realizar la simulación:
- Definir distribuciones de probabilidad para insumos financieros clave:
- Tasa de crecimiento de los ingresos:Distribución normal (media = 5%, desviación estándar = 2%)
- Costos operativos como % de ingresos:Distribución normal (media = 30%, desviación estándar = 5%)
- Tasa de descuento:Distribución normal (media = 8%, desviación estándar = 1%)
- Ejecutar 10.000 simulaciones, calculando el VPN para cada ejecución.
- Resumir resultados utilizando medidas estadísticas y visualizaciones.
Ahora, ejecutaré la simulación de Monte Carlo y generaré los resultados.
Simulación de Monte Carlo: Distribución del VPN
Resultados de la simulación de Monte Carlo
| Índice de crecimiento | Costo de operación % | Tasa de descuento | |
| contar | 10000.0 | 10000.0 | 10000.0 |
| significar | 0.050040570362915315 | 0.3002260181128686 | 0.07997808603004744 |
| estándar | 0.019910554247468792 | 0.04968107384600725 | 0.01008925573859806 |
| mín. | -0.01856183610533345 | 0.11544796696907525 | 0.04046458542990874 |
| 25% | 0.03640861533085948 | 0.26678017932445197 | 0.07319111966613821 |
Los resultados de la simulación de Monte Carlo ya están disponibles. El histograma muestra la distribución del Valor Actual Neto (VAN), destacando la incertidumbre financiera del proyecto. También puede explorar la tabla de estadísticas resumidas para revisar información clave, como la media, la desviación estándar y los valores percentiles del VAN, la tasa de crecimiento, los costos operativos y la tasa de descuento. ¡Avíseme si necesita más análisis o interpretaciones!
Conclusión: ¿Por qué la simulación de Monte Carlo es revolucionaria?
La simulación de Monte Carlo es Una de las herramientas más eficaces para la evaluación de riesgos y la previsión financiera.A diferencia de los modelos estáticos tradicionales, proporciona una visión probabilística de los resultados potenciales, ayudando a inversores y empresas a tomar decisiones basadas en datos.
Para simplificar las simulaciones de Monte Carlo y mejorar la precisión, SHEETS.MARKET ofrece plantillas profesionales que le permiten:
- Ejecute miles de simulaciones con sólo unos pocos clics.
- Visualizar distribuciones de riesgos instantáneamente.
- Personalizar modelos para sus necesidades financieras.
🚀 Ahorre tiempo y mejore la precisión: explore Hojas.Mercado ¡Para herramientas expertas de modelado financiero hoy mismo! Para obtener más información sobre modelos financieros, análisis de riesgos y simulaciones de Monte Carlo, síganos en LinkedInÚnase a la conversación y explore cómo estas herramientas pueden respaldar su proceso de toma de decisiones.